Squid Game and the Logic of Survival: A Game Theory Analysis
An Analysis of Cooperation, Defection, and Risk in a Deadly Game...
I was watching Squid Game Season 2 last week, just like the rest of the world has been lately, and while I was watching the voting scene, a light bulb appeared over my head... Can we explain this voting scene with game theory?
What was the scene?
In Squid Game, the voting scene highlights a critical moment where participants decide whether to continue the deadly competition or leave safely with a portion of the prize money collected so far. The prize money is accumulated as players progress through the games, with a set amount added to the pot for each player who is eliminated. The decision is based on majority rule: if the majority votes to leave, the game ends, and all players return home alive with their share of the accumulated prize pool; if the majority votes to stay, the game resumes, and everyone faces life-threatening risks in pursuit of the jackpot.
If you are interested, you can watch it from here: Voting Scene
My Struggles
At first, I tried to explain the dynamics with the Prisoner’s Dilemma, because it is basically my favorite concept in game theory. However, I later realized that there are not just two players in this game, and an individual decision is not that impactful on the result as it is in the Prisoner’s Dilemma. So, I started to explore majority games. Finally, I ended up with the Public Goods Game.
In this game, individuals decide whether to contribute to a shared resource that benefits everyone. While cooperation maximizes the collective good, individuals face an incentive to free-ride and not contribute, relying on others’ cooperation, which often leads to the under-provision of the public good.
The Voting Scene: A Modified Public Goods Game
Let’s start to conceptualize it to see how it works! Voting scene presents players with two options:
Cooperate (Vote to Leave): Prioritize collective safety by ending the game.
Defect (Vote to Stay): Risk their lives for the possibility of winning the prize money.
The outcome is determined by majority rule:
If the majority votes to leave, the game ends, and all participants return safely.
If the majority votes to stay, the game continues, forcing all players to participate further.
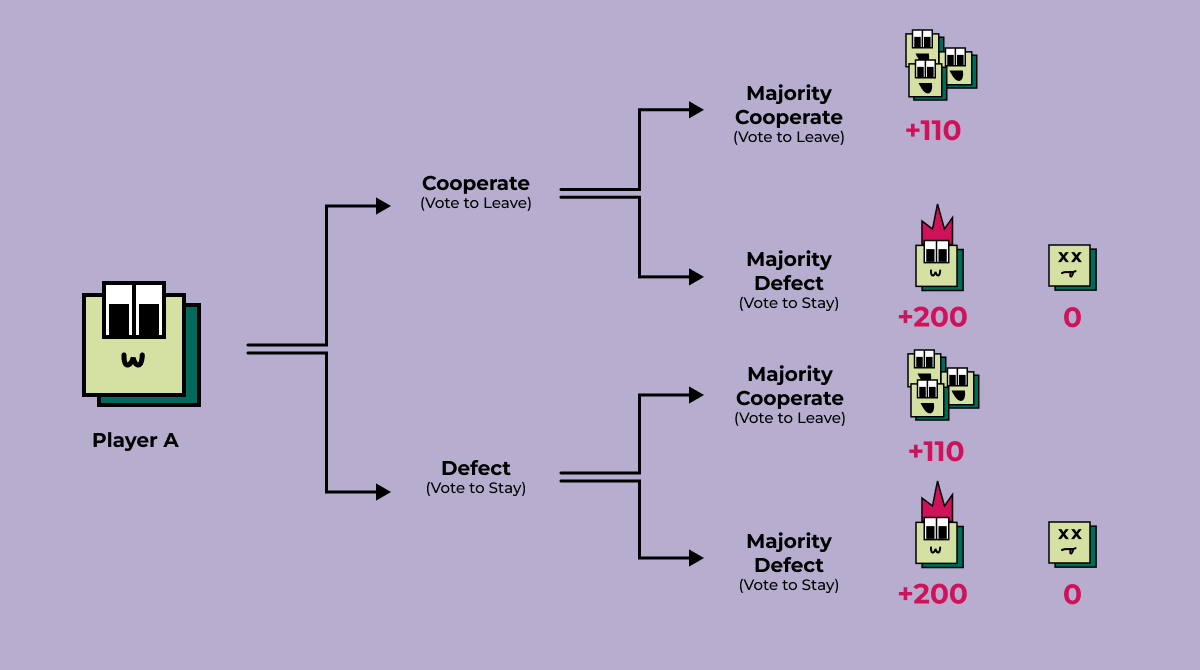
The Decision Tree
Here is the diagram of our voting process:
The decision tree begins with Player A’s choice: whether to cooperate (vote to leave) or defect (vote to stay). The outcome then branches based on the majority’s decision. Here’s how the payoffs are structured:
If Player A Cooperates:
If the majority also cooperates, everyone leaves the game safely with a +110 payoff (a share of the accumulated prize pool).
If the majority defects, Player A is forced to stay and faces the risks of continuing the game, which can result in either: +200 for winning or 0 for dying.
If Player A Defects:
If the majority cooperates, Player A is forced to leave safely with a +110 payoff like everyone else.
If the majority defects, Player A takes on the same risks of continuing the game as above: either +200 for winning or 0 for dying.
Best Option
This decision tree shows that the most reasonable choice is to cooperate. If the majority defects, you face the risk of dying and ending up with a payoff of 0. Considering the last game, where only 1 player out of 456 wins, the probability of winning is extremely low, making cooperation the safer and more rational choice.
What if?
What if Player A wants to maximize their chances of winning the jackpot? This is where an alternative strategy comes into play: Player A can defect and actively working to eliminate players who are likely to cooperate.
This reminds me the preemptive wars, it is when a country strikes first because it believes an attack from another country is imminent and wants to gain the upper hand by acting early. It’s like throwing the first punch in a fight you’re sure is about to happen, aiming to weaken your opponent before they can hit you.
Six Day War Analogy
One of the best examples to preempitve war is Six-Day War in 1967. Israel faced a coalition of Arab states (Egypt, Jordan, and Syria) preparing for war. Rather than wait for an attack, Israel launched a preemptive strike to neutralize their opponents’ military capabilities and in just six days, Israel achieved a decisive victory, gaining territorial and strategic advantages. Like Israel’s preemptive strategy, a player in Squid Game might defect and eliminate competitors before they can pose a significant threat. For example, by targeting cooperative players (who are more predictable and less aggressive), the defector reduces the pool of competition and increases their chances of winning.
In the Six-Day War, Israel’s victory came at the cost of long-term instability in the region and heightened distrust among neighboring states. Similarly, in Squid Game, aggressive defection can lead to distrust and retaliation, making survival in future rounds more difficult.
Brittanica
Conclusion
The voting scene in Squid Game brilliantly encapsulates the dilemmas of survival, trust, and strategy, mirroring real-world scenarios where individuals and nations grapple with cooperation and self-interest. It highlights how the fear of losing everything drives some to take extreme risks, while others cling to the safety of collective action.
Ultimately, Squid Game reminds us that survival isn’t just about strategy; it’s also about navigating the delicate balance between trust, fear, and ambition. In both games and life, every choice carries weight—not just for the individual but for the collective as well.
Please let me know what do you think about this analysis and comparison. If you want to support a growing publication, please subscribe and share the post!